高校数学で登場する関数のグラフや不等式の領域を描画できるソフト「GRAPES」で関数のグラフと不等式の領域を描画する
投稿日:
高校数学で登場する関数(三角関数、指数・対数関数など)のグラフや不等式の領域を描画したり、関数の変数がある値のときのグラフ上の点を表示させたりできるグラフ作成ソフト「GRAPES」を紹介します。今回は不等式の領域を図示したいと思います。もくじ
- 使い方
- 関数を定義する
- 定義した関数のグラフを描画する
- 不等式の領域を図示する
- グラフを画像としてエクスポートする
関数を定義する
GRAPESでは、ユーザーが任意の式を定め、それを使ってグラフを描画したり、不等式の領域を図示したりできます。また、GRAPESでは定義した関数の導関数(第二次まで)や不定積分をグラフにすることもできます。データパネルの「関数定義」についている「作成」ボタンを押しましょう。
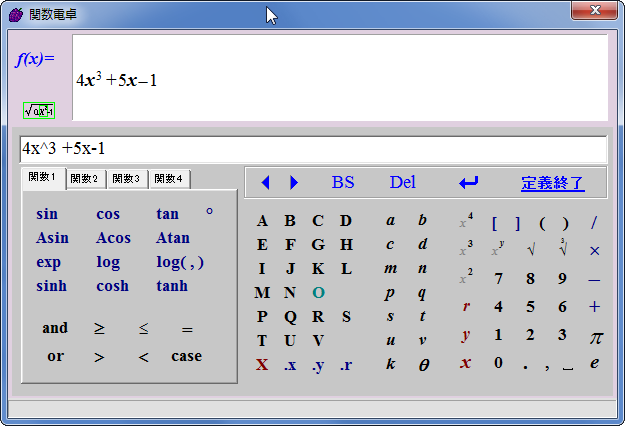
こんな感じで数式を入力し、「定義終了」を押せば関数が定義されます。
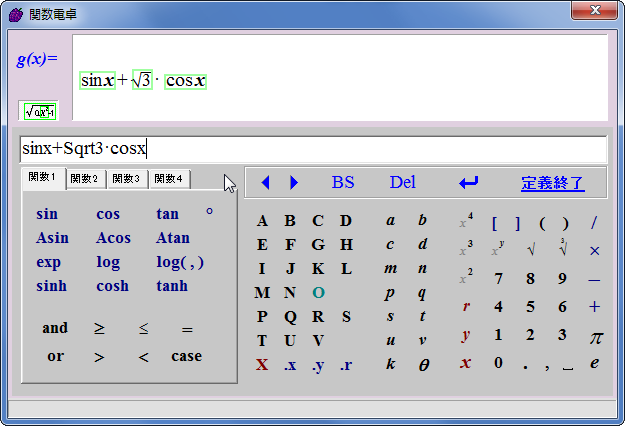
関数は複数個定義できます。
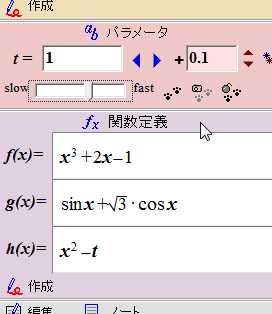
関数の中にx,y以外のパラメータを入れることもできます(その場合はパラメータ操作用のスライダーが表示されます)。
定義した関数のグラフを描画する
それでは、定義した関数を使ってy=f(x)のグラフを描画させます。データパネルの「関数」についている「作成」ボタンをクリックしましょう。
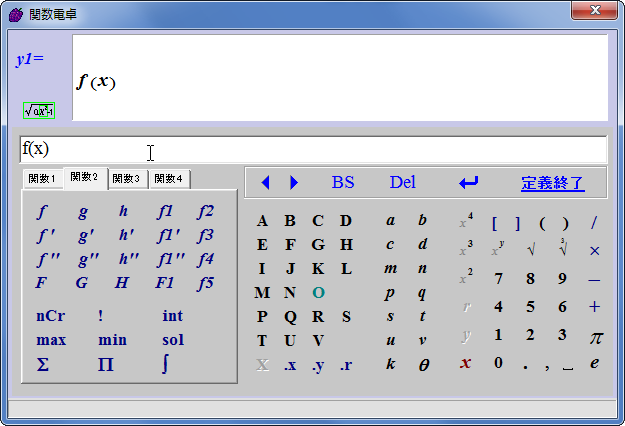
定義済みの関数を使う場合は、使用したい関数を選んで変数にxを入れるだけの簡単なお仕事です。ここで導関数や不定積分を選択すれば、対象の関数の導関数・不定積分のグラフが描画されます。
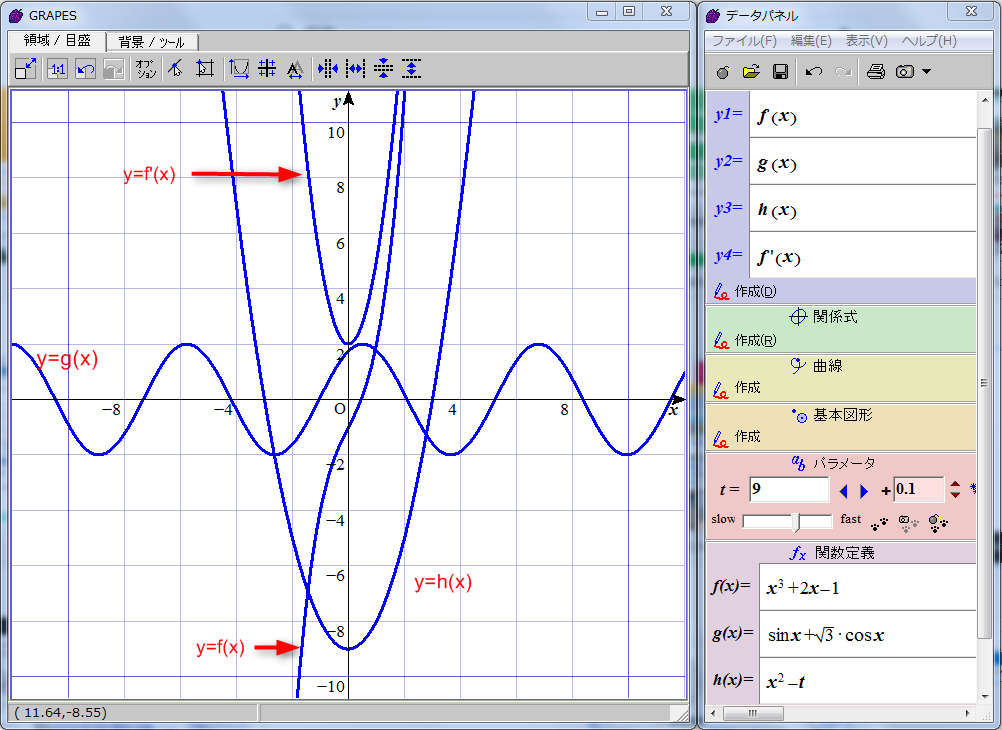
グラフを描画させました。
不等式の領域を図示する
それでは、定義した関数を使って不等式の領域を図示することにします。データパネルの「関係式」についている「作成」ボタンをクリックしましょう。
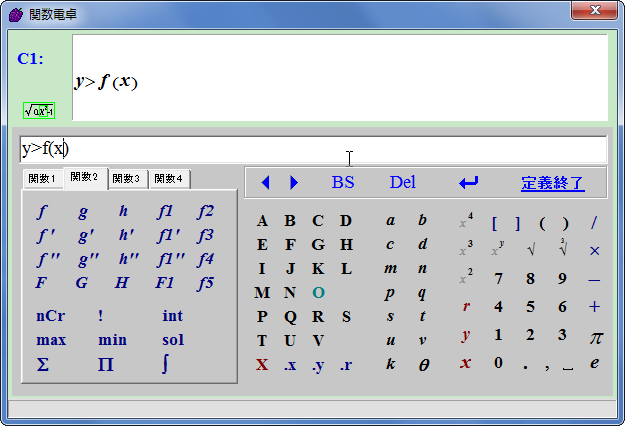
グラフのみを描画させる場合はyとf(x)を等号で結びましたが、今回図示するのは不等式の領域なので不等号を使います。
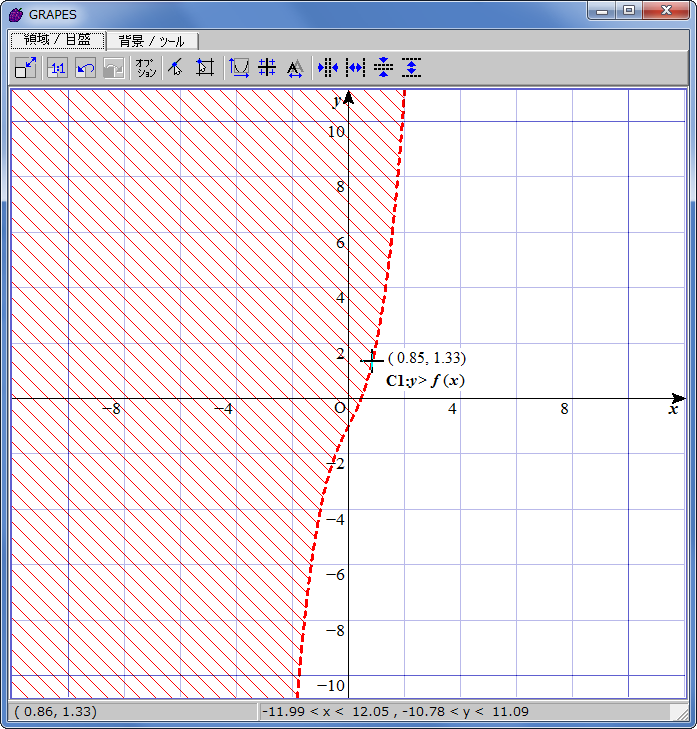
y>f(x) (f(x)=x^3+2x-1)の領域を図示できました。
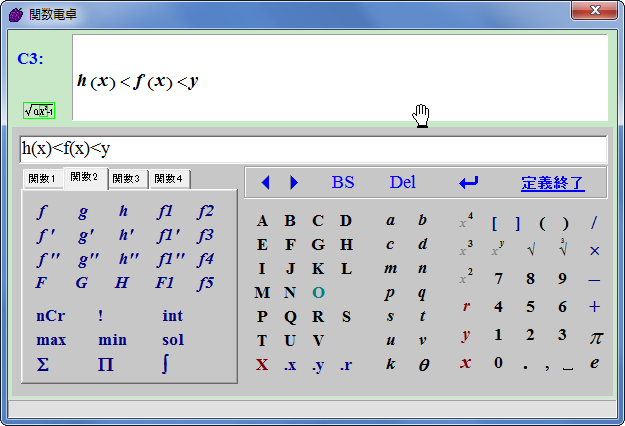
こんな風に、複数個の関数を絡めた不等式を入力しても領域を図示してくれます。
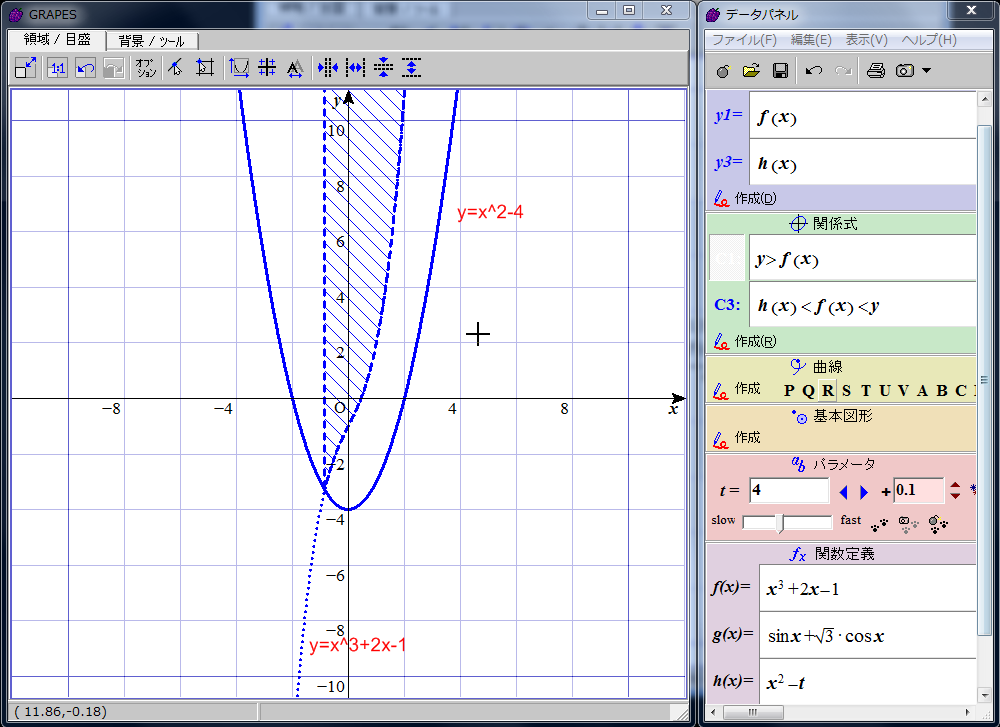
不等式だけだと領域を囲む線以外が描画されないこともあるので、その場合は適宜元の関数のグラフも書かせるといいかもしれません。
グラフを画像としてエクスポートする
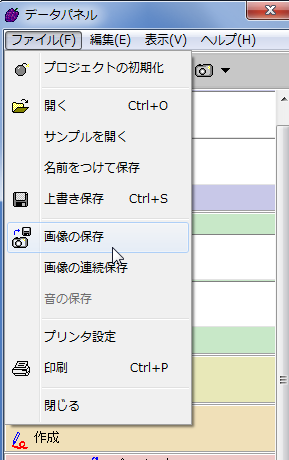
作成したグラフは、画像としてエクスポートすることもできます。エクスポートしたいグラフを作成した後、データパネルのツールバーにある「ファイル」→「画像の保存」をクリックすれば、グラフを画像として保存する画面が出ます。画像形式はビットマップやGIF,JPEG,PNGなどに対応しています。


